Fragestellung
Inhalt
Fragestellung¶
Ausgangslage¶
Sie haben ihr Studium beendet und gelten in ihrer Familie nun als Expert*in für finanzielle Fragestellungen. Ihr Onkel, der überraschend einen größeren Geldbetrag geerbt hat, kommt auf Sie zu und fragt Sie, wie er das Geld sinnvoll anlegen könne. Sie raten Ihm dazu, das Geld in einen breiten Aktienindex, d.h. passiv1, zu investieren. Ihr Onkel winkt direkt ab, weil ihm Aktien “viel zu riskant” seien. Da könne man ja auch sehr viel Geld bei verlieren.
Einerseits wollen Sie ihrem Onkel nicht raten das Geld in Immobilien oder in Festgeld zu investieren, da das Geld entweder zu wenig fungible oder zu gering verzinst wird. Anderseits kommen Sie selber ins Grübeln, ob eine Investition in Aktien nicht vielleicht doch (zu) riskant ist.
Sie beschließen deshalb der Frage empirisch nachzugehen.
Konkret wollen Sie analysieren, wie riskant eine Investition in Aktien tatsächlich ist. Obgleich es sich bei unserer Fragestellung um eine “persönliche” Analyse handelt, steht diese doch stellvertretend für ein typisches Business Analytics-Problem, bei dem es darum geht ein konkretes Problem bzw. eine konkrete Fragestellung datenbasiert zu beantworten.
Schritt 1: Konkrete Fragestellung¶
Für unsere Analyse bedarf es daher einer Fragestellung, die konkret bzw. “operationalisierbar” ist. Dies gilt für die bisherige Fragestellung leider noch nicht. Was bedeutet “riskant” bzw. “Risiko”? In welche Aktien wollen wir investieren? Wie lange wollen wir investieren?
Aus Vereinfachungsgründen definieren wir Risiko in unserem Fall als die Wahrscheinlichkeit einen Verlust zu erleiden. Wir fragen uns also konkret: Wie wahrscheinlich ist es, dass ihre Investition innerhalb von X Jahren an Wert verliert. Der Einfachheit halber nehmen wir an, dass wir in den DAX (siehe Wikipedia) investieren.
Die konkrete Fragestellung lautet also: Wie wahrscheinlich ist es, dass wir bei einer Investition in den DAX einen Verlust nach X Jahren erleiden?.
Lassen Sie uns nun überlegen, wie wir diese konkrete Frage empirisch beantworten können.
Schritt 2: Beschaffung der Daten¶
Die formulierte Frage ist natürlich nicht sicher bzw. eindeutig zu beantworten. Wir bräuchten dafür die DAX-Stände der nächsten Jahren; wir müssten also die Zukunft vorhersehen. Wir haben die perfekten Daten nicht.
In unserem Falle können wir jedoch historische Daten nutzen. Statt in die Zukunft zu schauen, treffen wir also eine Annahme. Für die Zwecke unserer Analyse nehmen wir an, dass die historischen Daten ein guter Schätzer für die Zukunft sind.
Historische Daten für Aktien sind glücklicherweise - zumindest für unsere Zwecke - einfach und frei zugänglich. Die Beschaffung der Rohdaten stellt also kein Problem dar.
“How to”: Download von Aktienkursen
Aktienkursdaten sind - zumindest für unsere Zwecke - einfach und kostenlos zugänglich. Wir werden als Quelle Yahoo Finance nutzen. Wir können hier (auch historische) Daten von allen wesentlichen Aktien und Indices einsehen und herunterladen. Die heruntergeladenenen Daten können in Form einer csv-Datei gespeichert werden2.
Hier ein Beispiel zum Download historischer DAX-Kurse:
Schritt 3: Aufbereitung der Daten¶
Die historischen Kursdaten als Datenquelle (“Rohdaten”) stellen kein Hürde dar. Der Download der Rohdaten ist einfach (siehe “💡 how to”), liefert jedoch nur bedingt eine Antwort auf unsere Frage. In Fig. 1 erkennen wir zwar, dass der DAX seit Beginn der Aufzeichnung Ende 1987 und bis zum Juli 2022 stark gestiegen ist (Anfangsstand: \(1.000\), Endstand: \(13.484\)) und wir unser Geld in etwa um den Faktor \(13x\) vermehrt hätten. Es gab jedoch offensichtlich auch Zeiträume in denen eine Investition an Wert verloren hätte. So hat der Dax z.B. seit seinem Höchststand von \(16.271,75\) im Januar 2022 bis heute deutlich an Wert verloren. Hätte man am Tag des Höchsttandes investiert, wäre ein deutlicher Verlust vereinnahmt worden.
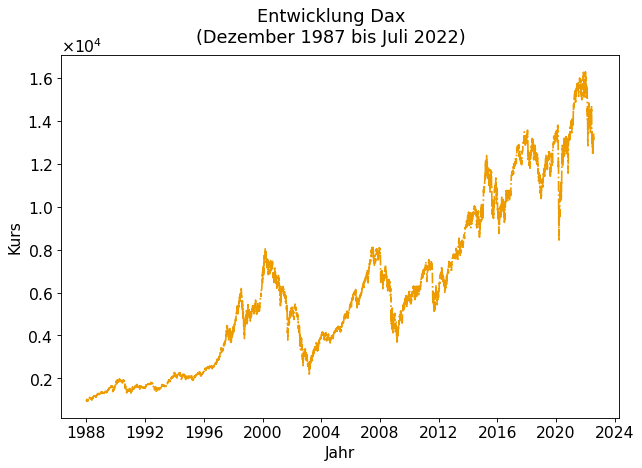
Fig. 1 Entwicklung Dax 1987 bis heute¶
Wir müssen die Rohdaten deshalb für unsere Zwecke aufbereiten. Was benötigen wir für unsere Zwecke konkret? Um diese Frage zu beantworten müssen wir darüber nachdenken, wie wir die Frage “Wie Wahrscheinlich ist es, dass wir in den DAX investieren und dabei einen Verlust erleiden? beantworten wollen.
Ansatz 1: Zurück in die Vergangenheit¶
Das Grundproblem ist, dass wir zwar historische Daten haben, wir aber theoretisch an jedem Tag in der Vergangenheit “zufällig” unser Geld hätten investieren können. Es gab sehr viele existierende Investitionsstrategie, die je nach Investitionszeitpunkt und -raum immer unterschiedliche “Gewinne” produziert hätten.
Beispiel 1: hätten wir am 10.6.1991 (Stand: \(1.698\)) investiert und am 26.03.2001 (Stand: \(5.726\)) verkauft, dann hätten wir eine Rendite von ca. \(+237\)% gemacht.
Beispiel 2: hätten wir am 12.04.2007 (Stand: \(7.808\)) investiert und am 19.12.2008 (Stand: \(4.696\)) verkauft, dann hätten wir eine Rendite von ca. \(-40\)% gemacht.
Die zwei Beispiele sind zufällig gewählt. Es hätte sehr viel mehr Zeitpunkte und Zeiträume gegeben, in der man hätte anlegen können. Dabei ist der optimalen Anlagezeitpunkt und Zeitraum leider erst im Nachhinein bekannt.
Um unsere Frage zu beantworten, müssen wir deshalb Zurück in die Vergangenheit gehen und für jeden möglichen Anfangszeitpunkt (d.h. jeder Handelstag seit Beginn des DAX in 1987) über jeden möglichen Anlagezeitraum investieren. Wir bilden also quasi alle historisch möglichen Anlagezeitpunkte und -räume ab. Aus diesen Daten könnten wir dann eine Aussage ableiten, wie oft wahrscheinlich es war, dass man nach X Jahren einen Verlust gemacht hat. Da wir in die Vergangenheit schauen, haben wir die Daten, um unsere Wertentwicklung für jede dieser Investitionen zu beobachten.
Lassen Sie uns zunächst anhand eines einfachen und fiktiven Beispiels durchspielen, welche Vergangenheitsanalyse wir durchführen wollen. Nehmen wir an, wir hätten \(10\) historische Kurse eines Index, dessen Entwicklung in Fig. 2 dargestellt sind.
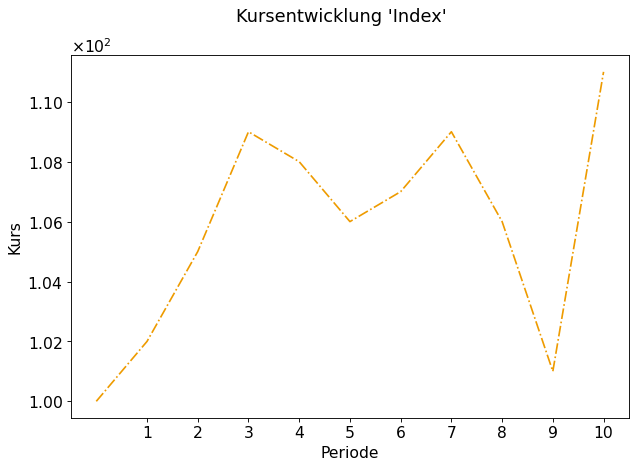
Fig. 2 Entwicklung Index über 10 Perioden¶
Wir fragen uns nun, wie Wahrscheinlich es war, einen Verlust zu vereinnahmen. Wir wollen mindestens 5 Perioden investieren (d.h. wir wissen noch nicht wie lange wir investieren wollen, sind uns jedoch sicher, dass wir innerhalb von 5 Perioden nicht verkaufen werden)
Die für unsere Überlegung benötigten Daten sind in Table 1 abgebildet.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|---|---|---|---|---|---|---|---|---|---|---|
Kurs |
102 |
105 |
109 |
108 |
106 |
107 |
109 |
106 |
101 |
111 |
Rendite |
2,0% |
3,0% |
4,0% |
-1,0% |
-2,0% |
1,0% |
2,0% |
-3,0% |
-5,0% |
10,0% |
Wir könnten insgesamt 6 verschiedene Investitionszeitpunkte definieren, die das Kriterium “mindestens 5 Perioden investieren” erfüllen.
Anlage 1: Kaufen in Periode 1
Anlage 2: Kaufen in Periode 2
…
Anlage 6: Kaufen in Periode 6
Wie ermitteln wir jetzt die Wertentwicklung unserer verschiedenen Anlagen über die Zeit?
Nehmen wir an, dass wir je \(1.00\) EUR investieren. Anlage 1 würde uns in der ersten Periode \(2\)% Rendite bringen. Aus unserer Anfangsinvestition würden also \(1\times(1+0.02) = 1.02\) EUR werden. Dieser neue Wert von \(1.02\) EUR würden sich in der nächsten Periode (Periode 2) mit \(3\)% verzinsen, so dass wir am Ende von Periode 2 insgesamt \(1.02 \times (1.03) = 1.0506\) EUR hätten. Diese Berechnung können wir für alle verfügbaren Perioden weiterführen.
Beispiel für Anlage 1 für 5 Perioden (\(I_0\) = Anfangsinvestition; hier: \(1\) EUR):
Über eine Haltedauer von 5 Perioden hätte man mit Anlage 1 demnach aus \(1.00\) EUR insgesamt \(1.06\) EUR gemacht, d.h. \(6\)ct verdient bzw. \(6\)% Rendite gemacht.
Allgemeiner können wir schreiben: die Performance einer Strategie (\(R_T\)) lässt sich über die Multiplikation der Perioden-Renditen ermitteln.
In Fig. 3 ist die Wertentwicklung der 6 Anlagen für alle möglichen Zeiträume bei einer Anfangsinvestition von je \(1.00\) EUR dargestellt.

Fig. 3 Entwicklung der sechs Anlagen¶
Im obigen Beispiel sehen wir, dass es für unseren Beispielindex Phasen gab, bei denen wir einen Verlust gemacht hätten. Z.B. hat Anlage 4 nach Periode 6 einen Verlust von ca. \(8\)ct. Auf der anderen Seite gab es Phasen, in denen man Gewinn gemacht hat. Z.B. Anlage 1 nach 10 Perioden.
Lassen Sie uns festhalten, wie wir die Rohdaten (Index-Stände) bearbeiten müssen, um eine Grundlage zur Beantwortung der Ausgangsfrage zu schaffen:
Renditen (\(R_t\)) aus Indexständen berechnen
kumulierte Produkte der Renditen (\(\prod (1 + R_t)\)) für jeden historisch möglichen Anfangszeitpunkt berechnen
In der praktischen Umsetzung schauen wir uns an, wie wir dies in Python umsetzen und welche Annahmen wir dafür treffen müssen.
Ansatz 2: Historischer Zufall¶
Im vorangeganen Beispiel haben wir gesehen, wie wir auf Basis von Vergangenheitsdaten fiktive Anlagen getätigt haben, die in der Form aber real möglich gewesen wären. So hätte man in der Vergangenheit tatsächlich in Periode 1 für z.B. 5 Perioden anlegen können. In diesem Fall hätte man tatsächlich eine Rendite von \(6\)% gemacht.
Der Nachteil dieses Ansatzes ist jedoch, dass es uns z.B. nicht möglich ist 6 unterschiedliche Anlagen mit einem Investitionshorizont von jeweils 10 Perioden abzubilden. Diese Anlagen wären in der Realität schlicht nicht möglich gewesen, da es in unserem Beispiel nur eine Anlage gibt, für die ein Investitionshorizont von 10 Perioden möglich war (Anlage 1).
Im zweiten Ansatz “Historischer Zufall” umgehen wir dieses Problem. Anstatt reale historische Performance abzubilden wählen wir ein anderes Vorgehen. Wir greifen wieder auf unseren Beispiel-Index (siehe Table 1 und Fig. 2) zurück. Anstatt alle real möglichen Anlagen zu untersuchen bzw. zu replizieren, werden wir alle real möglichen periodischen Renditen betrachten.
InTable 1 sind alle 10 tatsächlich entstandenen historischen Renditen dargestellt. Stellen Sie sich nun vor, wir hätten 10 Kugeln und auf jeder dieser Kugel stünde eine der 10 Renditen. Diese Kugeln legen wir nun in einen Korb, so dass wir die Kugeln nicht sehen können.
Nun stellen wir uns vor, wir hätten eine Anlage von \(1.00\) EUR für 3 Perioden getätigt. Wir fragen uns nun, was eine mögliche Wertentwicklung unserer Anlage gewesen sein könnte. Hierbei machen wir uns nun den Korb mit Kugeln zunutze. Wir nehmen eine Kugel aus dem Korb und notieren die darauf enthaltene Rendite. Danach legen wir die Kugel wieder zurück in den Korb und wiederholen den Prozess noch insgesamt zwei mal.
Wir haben also aus tatsächlich beobachtbaren historischen Renditen eine mögliche Wertentwicklung für unsere Anlage (zufällig) bestimmt. Diese könnte z.B. wie folgt aussehen:
Über die 3 Perioden haben wir aus \(1.00\) EUR insgesamt \(0.91\) EUR, d.h. einen Verlust von \(9\)ct gemacht. Es handelt sich hierbei um eine fiktive Wertentwicklung. Jedoch basiert diese auf historisch eingetretenen Renditen. Eine Wertentwicklung von z.B. \(+50\)% wäre z.B. in drei Perioden nicht möglich gewesen, da dies hohe Renditen je Periode erfordern würde, die so am Markt noch nicht aufgetreten sind.
Mit diesen Zufallsansatz können wir beliebig viele fiktive Anlagenverläufe erzeugen, die auf Basis der realen Renditen möglich sind.3
In der untenstehenden Darstellung (Fig. 4) sind \(10\) mögliche Wertentwicklung für eine Anlage von \(1.00\) EUR über \(10\) Perioden dargestellt.
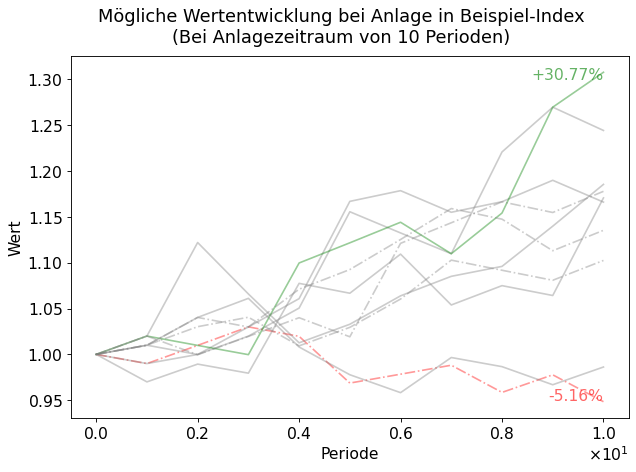
Fig. 4 Wertentwicklung von 10 Anlagen¶
Lassen Sie uns wieder festhalten, wie wir die Rohdaten (Index-Stände) bearbeiten müssen, um eine Grundlage zur Beantwortung der Ausgangsfrage zu schaffen:
Renditen (\(R_t\)) aus Indexständen berechnen
kumulierte Produkte der Renditen (\(\prod (1 + R_t)\)) für zufällig gezogene Renditen berechnen
In der praktischen Umsetzung schauen wir uns an, wie wir dies in Python umsetzen und welche Annahmen wir dafür treffen müssen.
Schritt 4: Analyse der Daten¶
Im nächsten Schritt müssen wir nun die Daten analysieren, um die Frage der Verlustwahrscheinlichkeit zu beantworten. Durch unsere konzeptionelle Vorarbeit ist dies der Schritt aber nicht mehr besonders groß.
Wir fragen uns nach der Verlustwahrscheinlichkeit zu einem Zeitpunkt X. Greifen wir unseren Beispiel-Index (siehe Table 1 und Fig. 2) auf und lassen Sie uns annehmen, dass wir die Verlustwahrscheinlichkeit nach 6 Perioden bestimmen möchten (d.h. X = 6). Eine naheliegende und deshalb nicht weniger sinnvolle Analyse wäre, zu untersuchen wie häufig eine Anlage einen Verlust erlitten hätte. Nehmen wir z.B. unsere 6 Anlagen aus Ansatz 1, so sehen wir, dass 2 der Anlagen in Periode 6 einen Wert von unter \(1.00\) EUR verzeichnen. Bei \(2\) von \(6\) Anlagen könnten wir also sagen, dass die Verlustwahrscheinlichkeit bei \(\frac{2}{6} \approx 33\)% lag. Schauen wir uns den zweiten Ansatz an, dann sehen wir dass auch dort nur \(2\) jedoch von \(10\) Anlagen in Periode 6 einen Verlust verzeichnen. Hier könnten wir also sagen, dass die Verlustwahrscheinlichkeit bei nur \(20\)% lag.
Fazit¶
Wir haben uns nun konzeptionelle Gedanken gemacht und die simple, aber vage Ausgangsfrage für uns - mit ein paar sinnvollen Annahmen - heruntergebrochen und sind so auf einen Lösungsansatz gekommen. Schauen wir uns den Lösungansatz an, dann stellen wir fest, dass die eigentlich Analyse - zumindest in unserem gewählten Ansatz - recht simple ist (im Grunde zählen wir nur). Dies ist keine Seltenheit. Oft ist die Datenaufbereitung und -strukturierung die im Vergleich zur eigentlichen Analyse deutlich komplexere und zeitaufwändigere Aufgabe; Schätzungen gehen davon aus, dass die Datenaufbereitung und -bereinigung ca. \(80\)% des gesamten Analyseprozesses ausm macht (siehe hierzu auch [DJ03]).
Schauen wir uns nun die Umsetzung in Python an.
- 1
In der Investment-Welt wird zwischen aktivem und passivem Investieren unterschieden. Bei ersterem werden “vielversprechende” Aktien identifiziert, die sich aus verschiedenen Gründen in der Zukunft vermeintlich gut entwickeln werden (z.B. Zukunftsbranche, gutes Management, etc.). Bei einer passiven Investitionsstrategie wird davon ausgegangen, dass die Identifikation von vielversprechenden Aktien nicht möglich ist, weil alle Informationen allen (professionellen) Kapitalanlegern zur Verfügung stehen und deshalb bereits im aktuellen Aktienkurs eingepreist sind. Deshalb wird stattdessen in breite Indizes investiert, um am Wirtschaftswachstum allgemein zu partizipieren. Weitere Informationen finden Sie z.B. hier.
- 2
Im weiteren Verlauf werden wir noch lernen, dass wir die Kurse via Python noch einfacherer und ohne manuelles Abspeichern von Daten einlesen können.
- 3
In unserem Beispiel über 3 Perioden gibt es insgesamt jedoch nur \(1.000\) unterschiedliche Wertentwicklung, da wir in jeder Periode \(10\) mögliche Renditen haben, d.h. es gibt insgesamt \(10\times10\times10=1.000\) Kombinationen.